Question

The time spent waiting in line is approximately normally distributed. The mean waiting time is 4 minutes and the standard deviation of the waiting time is 3 minutes. Find the probability that a person will wait for more than 1 minute. Round your answer to four decimal places.

Answer 1

Given:

`\begin{gathered} \mu=4\text{ minutes} \\ \sigma=3\text{ minutes} \\ x=1\text{ minute} \end{gathered}`

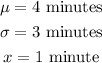
Using the Z-score formula, the Z-score of the data is gotten below.

`Z=(x-\mu)/(\sigma)`

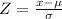
Hence,

`\begin{gathered} Z=(1-4)/(3) \\ Z=(-3)/(3) \\ Z=-1 \end{gathered}`

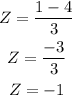
From the Z-scores table, the probability that a person will wait for more than 1 minute is;

`\begin{gathered} P(x>Z)=0.84134 \\ \\ To\text{ four decimal places;} \\ P(x>Z)=0.8413 \end{gathered}`

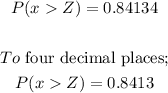
Therefore, to four decimal places, the probability that a person will wait for more than 1 minute is 0.8413