Question

The critical values of x for f(x)=2x^3-15x^2+36 x are?

Answer 1

Answer: 3 and 2

First, find the derivative of the given function

`f(x)=2x^3-15x^2+36x`
`f^(\prime)(x)=6x^2-30x+36`

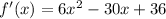
Next, solve for x

`f^(\prime)(x)=6x^2-30x+36`

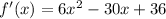
*Factor out 6 and equate to 0

`6(x^2-5x+6)=0`
`6(x-3)(x-2)=0`

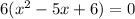
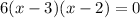
*Divide both sides by 6.

`(x-3)(x-2)=0`

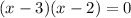
*Set x - 3 = 0

`x-3=0`
`x=3`

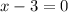
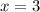
*Set x - 2 = 0

`x-2=0`
`x=2`

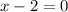
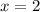
Next, substitute these x values to the original function.

* x = 3

`x=3`
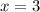
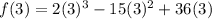
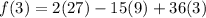
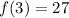
`f(x)=2x^3-15x^2+36x`
`f(3)=2(3)^3-15(3)^2+36(3)`
`f(3)=2(27)-15(9)^{}+36(3)`
`f(3)=54^{}-135+108`
`f(3)=27`

* x = 2

`x=2`
`f(2)=2(2)^3-15(2)^2+36(2)`
`f(2)=2(8)^{}-15(4)^{}+36(2)`
`f(2)=16^{}-60^{}+72`
`f(2)=28`

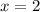
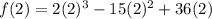
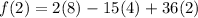
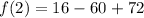
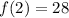
We now have a set of critical points

( 3, 27 ) and ( 2, 28 )

The critical values of x would be 3 and 2.