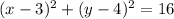The equation of a circle is:

where (h,k) is the center of the circle and r the radius. In this case we know the center (3,4) 1*but we don't know the radius, then we have to find it first.
To find the radius we need to use the fact that the circle is tangent to the x-axis. We know that the distance from a point (h,k) to a line Ax+By+C=0 is given by:
![d=\frac{\lvert Ah+Bk+C\rvert}{\sqrt[]{A^2+B^2}}](https://img.qammunity.org/2023/formulas/mathematics/college/1rv0vj2umaa1u9jqcxu9of6u44g963tz90.png)
Now, the x axis has equation y=0; this means that A=0, B=1 and C=0. then we have:
![d=\frac{\lvert1\cdot4\rvert}{\sqrt[]{1^2^{}}}=(4)/(1)=4](https://img.qammunity.org/2023/formulas/mathematics/college/wxi2zs3s2dsn5rbhtioz3ey1k5uuknp0cg.png)
This means that the radius is 4.
Once we have the radius we plug its value and the value of the center in the equation, then:
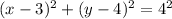
Therefore, the equation is: