Question

7. Maxine collected data on the number of students enrolled in 8th grade math class at Abby's Flying fairy school. Which statement is true regarding the range of her data?

Answer 1

Given the data as shown in the table:

Range = max - min = 28 - 20 = 8

The mean of the data = Sum/number

The sum of the data = 20 + 22 * 4 + 28 * 2 = 164

The number of the data = 1 + 4 + 2 = 7

So, the mean of the data = 164/7 = 23.43

The standard deviation will be :

The numerator =

`(20-23.43)^2+4\cdot(22-23.43)^2+2\cdot(28-23.43)^2=61.714`

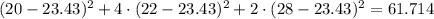
So, the standard deviation =

`\sqrt[]{(61.714)/(7-1)}=\sqrt[]{(61.714)/(6)}=3.207`

So,

range = 8

mean = 23.43

SD = 3.207

So,

The answer is: option (2) : range < mean