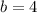- The Slope-Intercept form of the equation of a line is:

Where "m" is the slope of the line and "b" is the y-intercept.
- The Point-Slope form of the equation of a line is:

Where "m" is the slope and this is a point on the line:
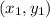
You know that (according to the information given in the exercise):
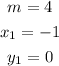
Then, you can determine that the equation of that line in Point-Slope form is:
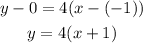
In order to write it in Slope-Intercept form, you only need to simplify the right side of the equation applying the Distributive property. Then, you get:
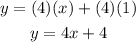
You can identify that:
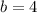
Then, the answers are:
- Equation in Point-Slope form
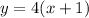
- Equation in Slope-Intercept form
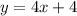
- The y-intercept