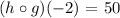1 Answer

Shabany · Answer 1 · 2023-04-24T12:42:29+0000

Solution:

Let the following functions:

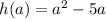
and

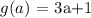
$g(a)\text{ = 3a+1}$

notice that the composition of the above function is :

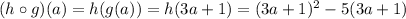
$(h\circ g)(a)=h(g(a))=h(3a+1)=(3a+1)^2-5(3a+1)$

this is equivalent to:

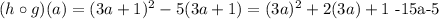
$(h\circ g)(a)=(3a+1)^2-5(3a+1)=(3a)^2+2(3a)+1\text{ -15a-5}$

this is equivalent to:

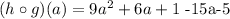
$(h\circ g)(a)=9a^2+6a+1\text{ -15a-5}$

putting together the similar terms, we get:

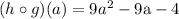
$(h\circ g)(a)=9a^2-9\text{a}-4$

now, replacing a = -2 in the above equation, we get:

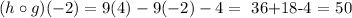
$(h\circ g)(-2)=9(4)^{}-9(-2)-4=\text{ 36+18-4 = 50}$

then, we can conclude that the correct answer is:

$(h\circ g)(-2)\text{ = 50}$

Please log in or register to add a comment.