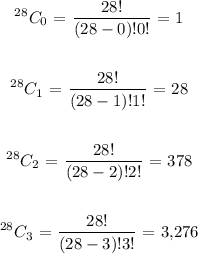The coefficients of the first four terms of the expression are 1,28,378 and 3,276
Here, we want to get the coefficients of the first 4 terms
We start as follows;
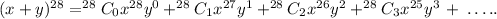
The coefficients are simply the combination parts
By calculating using the combinatorial formula, we can have the coefficients
The general formula for calculating the combination of two numbers is simply;
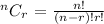
We now proceed to apply the formula above to each of the combination expressions in the expansion
We have this as follows;