The slope intercept formula is given by the expression below:

Where "m" is the slope and b is the y-intercept of the graph.
The first step to solve this problem is to rewrite the given expression in it's slope-intercept form. This is done below:
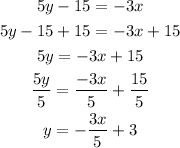
From the expression we know that the y-intercept is "3". We need another point to graph the equation correctly. To find it we will make y=0 and find the value of x.

We can finally graph the equation. It crosses the y-axis at "3" and the x-axis at "5".