Question

What is the use of the 8.00 and 3.00 and lastly the 4.50

Answer 1

Let's define the following variables.

x = amount of $8 sparkling water

y = amount of $3 sparkling water

z = amount of $4.50 sparkling water

If we want to create 200 gals of sparkling water then we can form the equation below:

`x+y+z=200gal`

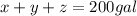
"She must use twice as much of the $4.50 water as the $3.00 water" means the amount of z must be twice to equate to y.

`z=2y`

Using the value of y, we can rewrite equation 1 as:

`\begin{gathered} x+y+2y=200 \\ x+3y=200 \end{gathered}`

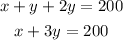
Then, applying the cost per gallon in each type of sparkling water, we have another equation:

`\begin{gathered} 8x+3y+4.50z=200(5) \\ 8x+3y+4.50z=1000 \\ 8x+3y+4.50(2y)=1,000 \\ 8x+3y+9y=1000 \\ 8x+12y=1000 \end{gathered}`

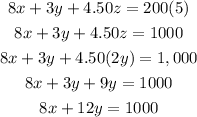
To summarize, we have:

Equation 1: x + 3y = 200

Equation 2: 8x + 12y = 1000

Graphing these two equations, we get:

The intersection of the two equations is at (50, 50)c

Therefore, the value of x = 50 gallons and the value of y = 50 gallons.

Now, since z = 2y, ten xz = 2(50) = 100 gallons. z = 100 gallons

In conclusion,

50 gallons of $8.00 sparkling water

50 gallons of $3.00 sparkling water

100 gallons of $4.50 sparkling water