Question

A 3.00-kg object is initially moving northward at 15.0 m/s. Then a force of 15.0 N, toward the east, acts on it for 3.40 s.A. At the end of the 3.40 s, what is magnitude of the object’s final velocity? ( m/s ) B. What is the direction of the final velocity? Enter the angle in degrees where positive indicates north of east and negative indicates south of east. ( ° )C. What is the change in momentum during the 3.40 s? Take +y to be north and +x to be east. Enter a positive answer if the change in momentum is toward east and a negative answer if the change in momentum is toward west. ( kg·m/s)

Answer 1

Given:

Mass, m = 3.00 kg

Inital velocity, Vy = 15.0 m/s northward

Force, Fx = 15.0 N towards east

time, t = 3.40 s

Let's solve for the following:

• (A). At the end of the 3.40 s, what is magnitude of the object’s final velocity?

First find the acceleration towards east using the formula:

`\begin{gathered} a_x=(F_x)/(m) \\ \\ a_x=(15.0)/(3.00) \\ \\ a_x=5m/s^2 \end{gathered}`

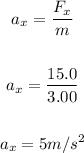
Where:

Initial velocity towrads east = Vox = 0 m/s

Hence, to find the final velocity towards east after the 3.40 seconds, we have:

`\begin{gathered} v_x=v_(ox)+at \\ \\ v_x=0+5(3.40) \\ \\ v_x=17\text{ m/s} \end{gathered}`

Now, to find the magnitude of the object's final velocity, apply the formula:

`v=\sqrt[]{v^2_x+v^2_y}_{}_{}`

Where:

Vx = 17 m/s

Vy = 15.0 m/s

We have:

`\begin{gathered} v=\sqrt[]{(17)^2+(15)^2} \\ \\ v=\sqrt[]{289+225} \\ \\ v=\sqrt[]{514} \\ \\ v=22.7\text{ m/s} \end{gathered}`

Therefore, the magnitude of the object's final velocity is 22.7 m/s.

• (B). What is the direction of the final velocity?

To find the direction of the final velocity, apply the formula:

`\tan \theta=(v_y)/(v_x)`

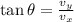
Thus, we have:

`\begin{gathered} \tan \theta=(15)/(17) \\ \\ \theta=\tan ^(-1)((15)/(17)) \\ \\ \theta=+41.4^0 \end{gathered}`

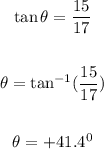
Thererfore, the direction of the fianl velocity is 41.4 degrees North of East.

• (C). What is the change in momentum during the 3.40s?

The change in momenutum in the y-component is = 0

Apply the formula to find the change in x-component:

`\Delta p_x=m\Delta v_x`

Thus, we have:

`\begin{gathered} \Delta p_x=(3.00)(17) \\ \\ \Delta p_x=51\text{ kg m/s} \end{gathered}`

Therefore, the change in momentum is 51 kg m/s towards east.

ANSWER:

• (a). 22.7 m/s

,

• (b). +41.4 degrees

,

• (c). +51 kg. m/s