ANSWER and EXPLANATION
a) We want to solve the quadratic equation by completing the square:
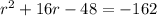
The first step is to add 48 to both sides of the equation to eliminate -48 from the left-hand side:
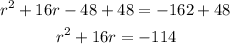
Now, to complete the square, divide 16 by 2 and find the square. Then, add that to both sides of the equation:
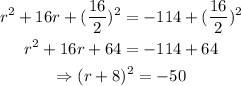
That is the equation after completing the square.
To find the solutions of r, find the square root of both sides of the equation and simplify:
![\begin{gathered} r+8=\sqrt[]{-50} \\ r+8=\pm5\sqrt[]{2}i \\ \Rightarrow r=-8+5\sqrt[]{2}i;r=-8-5\sqrt[]{2}i \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/exkyfq302ntv8zcruwla51acvmqhqdqxda.png)
Those are the solutions.
b) We want to solve the quadratic equation given by completing the square:
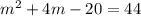
The first step is to add 20 to both sides of the equation to eliminate -20 from the left-hand side:
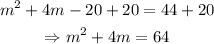
Now, to complete the square, divide 4 by 2 and find the square. Then, add that to both sides of the equation:
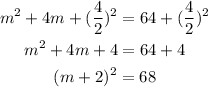
That is the equation after completing the square.
To find the solutions of m, find the square root of both sides of the equation and simplify:
![\begin{gathered} m+2=\sqrt[]{68} \\ m+2=\pm2\sqrt[]{17} \\ \Rightarrow m=-2+2\sqrt[]{17};m=-2-2\sqrt[]{17} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/yyyuwavohowznpw3ekkwuxnbklqwv37yxa.png)
Those are the solutions.