Question

The annual inventory cost C for a manufacturer is given below, where Q is the order size when the inventory is replenished. Find the change in annual cost when Q is increased from 353 to 354, and compare this with the instantaneous rate of change when Q = 353. (Round your answers to two decimal places.)

Answer 1

The given equation is

`C=(1014000)/(Q)+5.8Q`

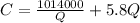
To find the increase from 353 to 354, substitute Q by these values, then subtract the answers

`\begin{gathered} Q=353 \\ I.C=\lbrack(1014000)/(354)+5.8(354)\rbrack-\lbrack(1014000)/(353)+5.8(353)\rbrack \end{gathered}`

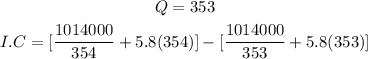
Calculate it

`\begin{gathered} I\mathrm{}C=\lbrack4917.60678\rbrack-\lbrack4919.921246\rbrack \\ I\mathrm{}C=-2.314466459 \end{gathered}`

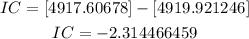
Round it to 2 decimal places

I.C = -2.31

Now we will find C' using derivative

`\begin{gathered} C=1014000Q^(-1)+5.8Q \\ C^(\prime)=1014000(-1)Q^(-1-1)+5.8(1)Q^(1-1) \end{gathered}`

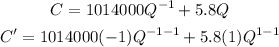
Simplify each term

`\begin{gathered} C^(\prime)=-1014000Q^(-2)+5.8Q^0 \\ C^(\prime)=-(1014000)/(Q^2)+5.8 \end{gathered}`

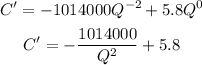
Substitute Q by 353

`\begin{gathered} C^,=-(1014000)/((353)^2)+5.8 \\ C^(\prime)=-2.337453956 \end{gathered}`

Round it to the nearest 2 decimal place

`C^(\prime)(353)=-2.34`

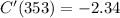
The answer is

Change in C = -2.31

C'(353) = -2.34