ANSWER
(x - 1)² + (y - 3)² = 36
Step-by-step explanation
The equation of a circle in standard form is,

Where (h, k) is the center of the circle and r is its radius.
As stated in the question, we have to complete the squares to find the equation of this circle in standard form. This means that we have to find a way to write the terms that contain each variable - x and y, in the form of a perfect binomial squared,
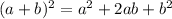
In the equation in general form, note that both x² and y² have the same coefficient, 3, and that all the other coefficients are multiples of 3. So, first, divide both sides of the given equation by 3,
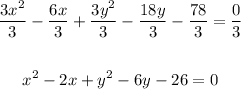
Now, let's take the terms that contain x: x² - 2x. As we can see, the first term of the binomial will be x, and the second term of the expanded form is -2x, so the second term of the binomial is,
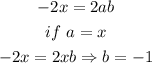
Hence, the binomial that contains x is (x - 1)², which expanded is,
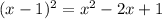
To replace the first two terms of the equation of the circle with this binomial we have to add and subtract 1, to keep the equality,
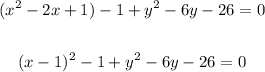
Similarly, for the terms that contain y: y² - 6y, we have that the first term of the binomial is y, and, if the second term of the expanded form is -6y, then the second term of the binomial is,
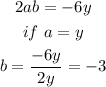
Hence, the binomial that contains y is (y - 3)², which expanded is,
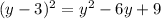
So, as we did with the binomial containing x, we have to add and subtract 9 to the equation of the circle to be able to replace the terms that contain y by this binomial squared,
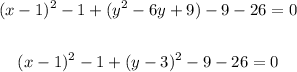
Finally, combine like terms,
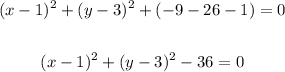
And add 36 to both sides,
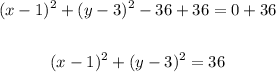
Hence, the standard form of the equation of this circle is (x - 1)² + (y - 3)² = 36, and the radius of the circle is 6, since 6² = 36.