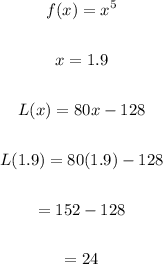Question

10 attempts remaining.(1 point) Use linear approximation, i.e. the tangent line, to approximate 1.9^5 as follows:Let f(x) = x^5. The equation of the tangent line to f(x) at x = 2 can be written in the form y = mx + bwhere m is:-and where b is:Using this, we find our approximation for 1.9^5 is

Answer 1

Given:

`f(x)=x^5`

Tangent of line f(x) is at x=2

Line is:

`y=mx+b`

Find-:

Value of b, m.

Sol:

The slope of the line tangent to

`f(x)=x^5`

is the derivative function.

The derivative function uses the power rule.

`\begin{gathered} f(x)=x^5 \\ \\ f^(\prime)(x)=5x^4 \end{gathered}`

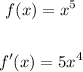
So at x=2

`\begin{gathered} f^(\prime)(x)=5x^4 \\ \\ f^(\prime)(2)=5(2)^4 \\ \\ f^(\prime)(2)=80 \end{gathered}`

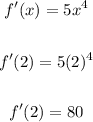
The function value for x=2 is:

`\begin{gathered} f(x)=x^5 \\ \\ f(2)=2^5 \\ \\ f(2)=32 \end{gathered}`

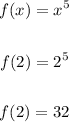
At x=2 coordinates is:

`(x_1,y_1)=(2,32)`

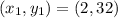
So the general equation of a line is:

`\begin{gathered} y-y_1=m(x-x_1) \\ \\ y-32=80(x-2) \end{gathered}`

Solve for m and b is:

`\begin{gathered} y-32=80(x-2) \\ \\ y-32=80x-160 \\ \\ y=80x-160+32 \\ \\ y=80x-128 \end{gathered}`

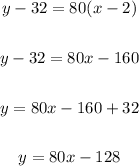
Compare with the general equation:

`\begin{gathered} y=mx+b \\ \\ y=80x-128 \end{gathered}`

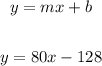
So value is:

`\begin{gathered} m=80 \\ \\ b=-128 \end{gathered}`

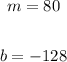
So, the linear approximation of 1.9^5

`\begin{gathered} f(x)=x^5 \\ \\ x=1.9 \\ \\ L(x)=80x-128 \\ \\ L(1.9)=80(1.9)-128 \\ \\ =152-128 \\ \\ =24 \end{gathered}`