Question

How do we do this one plkz ia sked braily already they got it wrong

Answer 1

1)

In general, given a function f(x), f'(a) is the slope of the tangent line to the graph of f(x) at x=a.

Thus, in our case, calculating the derivative of y(x),

`\begin{gathered} y=5+cot(x)-2csc(x) \\ \Rightarrow y^(\prime)(x)=-csc^2x-2(-cot(x)csc(x))=-csc^2x+2cot(x)csc(x) \end{gathered}`

Then, evaluate y'(x) at the x-coordinate of point P (x=pi/2), as shown below

`y^(\prime)((\pi)/(2))=-(1)^2+2*0*1=-1`

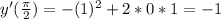
Therefore, the slope of the tangent line to the curve at P is equal to -1.

Calculating the equation of such line given its slope and a point on it,

`\begin{gathered} P=((\pi)/(2),3),m=-1 \\ \Rightarrow y-3=-1(x-(\pi)/(2)) \\ \Rightarrow y=-x+(\pi)/(2)+3= \end{gathered}`

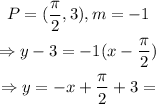
The answer to the first part is y=-x+(6+pi)/2, which is equivalent to y=-x+pi/2+3

(pi/2+3=4.570796...)

2)According to the question, the line is the horizontal tangent to the curve at Q; therefore, its slope is equal to zero because it is horizontal.

Then, we need to find the y-coordinate of point Q. Notice that the x-coordinate of point Q is 1; thus,

`y(1)=5+cot(1)-2csc(1)\approx3.2653...`

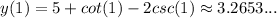
Therefore, the exact equation is y=5+cot(1)-2csc(1), or approximately y=3.2653...