Question

I’m confused on this question and looking for an answer.

Answer 1

We are given the following information.

m∠ROP = 125°

We are asked to find the measure of each arc in the circle.

Arc RP:

The arc RP can be found by applying the central angle theorem.

`\begin{gathered} Central\;angle=Intercepted\;minor\;arc \\ m\angle ROP=mRP \\ 125\degree=125\degree \end{gathered}`

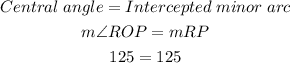
m∠ROP is a central angle with an intercepted minor arc from A to B.

Therefore, the arc RP is 125°.

Arc QS:

The arc QS must be equal to the arc RP since the circle is divided into halves.

Therefore, the arc QS is also 125°.

Arc QR and SP:

Notice that the central angles m∠QOR and m∠SOP are congruent.

Recall the theorem that congruent central angles have congruent arcs.

Let x represent arc QR and arc SP.

`\begin{gathered} mRP+mQS+QR+SP=360\degree \\ 125\degree+125\degree+x+x=360\degree \\ 250\degree+2x=360\degree \\ 2x=360\degree-250\degree \\ 2x=110\degree \\ x=(110\degree)/(2) \\ x=55\degree \end{gathered}`

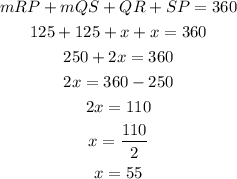
Therefore, arc QR = 55° and arc SP = 55°