Question

2. f(x) = |x| - 6quations.n.Vertex :Domain :Range :Max/Min :x-intercept:y-intercept:

Answer 1

This is an abolute value function, which means it will have a vertex for when "x" is equal to 0. If we apply this to the function we will find:

`f(0)=|0|-6=-6`

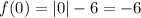
Vertex: -6

The domain of the function are all the possible values that can be used as an input. Which are all the real numbers.

The range of the function are all the possible values that can be an output of the function. These are given by [-6, infinity), because every negative value of "x" that is used as an input will be applied to the absolute value operator resulting in a positive number. So the output can only be negative for when the value of x is less than "-6".

Max/Min: The maximum of the funcion is infinity, because the larger the number used as an input the larger the ouput will be. The minimum value of the function is -6, it is given by the vertex.

x-intercept: It's when the value of the function is equal to "0". To find it we need to make "f(x)=0" and solve the expression:

`\begin{gathered} 0=|x|-6 \\ |x|=6 \\ x_1=6 \\ x_2=-6 \end{gathered}`

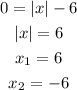
The function will cross the x-axis twice, on "x=6" and "x=-6".

y-intercept: It's when the value of "x" is equal to zero. To find it we need to calculate the value of the function when x=0.

`\begin{gathered} f(0)=|0|-6 \\ f(0)=-6 \end{gathered}`

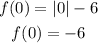
The y-intercept happens at y=-6.