At first, we have to find y', then find y'(2)
The given equation is
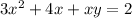
We want to use the rule of the product in differentiation
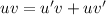
Then to differentiate xy, it will be
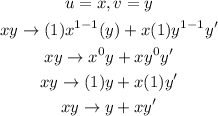
We will differentiate it with respect to x
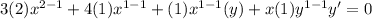
Simplify each term

Now, we need to separate y' on the side and the other terms on the other side
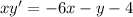
Divide them by x

We need to find y'(2) by substitute x by 2 and y by -9
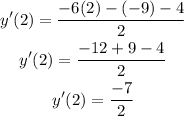
The answer is -7/2