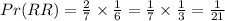First Independent event:
Consider a bag that contains 4 blue balls and 2 red balls. If we pick a ball two times with replacement, the event of picking a blue the first time is independent of the event of picking blue a second time. Therefore, the probability of picking a blue ball the first time and the second time is given by:
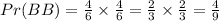
Second Independent event:
Consider a bag that contains 1 blue ball and 5 red balls. If we pick a ball and a red-colored card from a standard deck, the event of picking a blue ball is independent of the event of picking a red card. Therefore, the probability of picking a blue ball and a red card is given by:
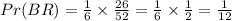
First Dependent event:
Consider a group of motorcycles such that 4 are American made, 4 are German made and 5 are Japanese made. If we select a motorcycle from the group, then another motorcycle without putting the first one back, what is the probability that the first motorcycle is Japanese made and the second is German made.
The probability is given by
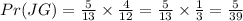
Second Dependent event:
Consider a bag that contains 5 blue balls and 2 red balls. If we pick a ball from the bag, then another without replacement, what is the probability of picking a red ball the first time and another red ball the second time.
The probability is given by