Question

If 1 - 2i is a root of 3x2 + ax + b = 0, find the value of b.

Answer 1

In the quadratic equation

`ax^2+bx+c=0`

It has two roots, their sum = -b/a

their product is c/a

In our question the quadratic equation is

`3x^2+ax+b=0`

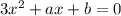
So the product of its root is b/3

One of the two roots is (1 - 2i), then the other root must be (1 + 2i)

Because its roots must be conjugate numbers

Let us find its product and equate it by b/3

(1 - 2i)(1 + 2i) = (1)(1) + (1)(2i) + (1)(-2i) + (-2i * 2i) = 1 +2i - 2i - 4i^2

2i + -2i = 0

i^2 = -1, then

(1 - 2i)(1 + 2i) = 1 - 4(-1) = 1 + 4 = 5

Equate b/3 by 5

`\begin{gathered} (b)/(3)=5 \\ b=15 \end{gathered}`

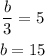
The value of b is 15