Question

what to do: look at the equation and match each answer to the answer choice answers -the function has x-intercepts? -one vertical asymptote along the line where x always equals what number -one horizontal asymptote along the line where y always equals what number -how many holes? - there is a hole where the y intercept should be

Answer 1

Given:

`y=(9x^2+81x)/(x^3+8x^2-9x)`

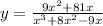
The graph of the function is shown;

1) x-intercepts

From the graph of the equation, there is no x-intercept because the curve does not cut the x-axis at any point.

2) Vertical asymptote

The vertical asymptote is the vertical line the curve tends towards but does not touch.

From the graph, the vertical asymptote is at x = 1.

3) Horizontal asymptote

The horizontal asymptote is the horizontal line the curve tends towards but does not touch.

From the graph, the horizontal asymptote is at y = 0.

4) Hole

To get the hole, we get the common factor.

`\begin{gathered} y=(9x^2+81x)/(x^3+8x^2-9x) \\ y=(9x\left(x+9\right))/(x\left(x-1\right)\left(x+9\right)) \\ The\text{ common factors are;} \\ x\text{ and }x+9 \\ \\ Equate\text{ the common factors to zero} \\ Hence,\text{ there is a hole at}x=0 \\ \\ \\ \\ x+9=0 \\ Also,\text{ there is a hole at}x=-9 \\ \\ \\ Hence,\text{ cancelling out the common terms, the equation becomes;} \\ y=(9)/((x-1)) \\ when\text{ x = 0,} \\ y=(9)/(0-1)=(9)/(-1) \\ y=-9 \\ Hence,\text{ hole is at }(0,-9) \\ \\ \\ Also,\text{ when x = -9} \\ y=(9)/(-9-1)=(9)/(-10) \\ Hence,\text{ hole is also at }(-9,-(9)/(10)) \end{gathered}`

Therefore, there are two holes.

A hole exists at (0,-9) which is where the y-intercept should be because the y-intercept usually exists at the point x = 0. Hence, there is a hole where the y-intercept should be. TRUE