SOLUTION
(a) To break even, total revenue must be equal to total cost.
So we equate the revenue function to the cost function and find x which is the number of units, we have
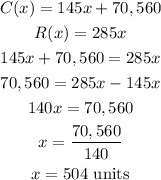
Hence number of units sold to break even is 504 units
Amount coming and going out, we put x for 504 into any of the equation, we have
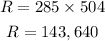
Hence the answer is 143,640
The profit function, we subtract cost function from revenue, we have
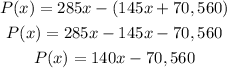
Hence the answer is
P(x) = 140x - 70,560