If two lines are perpendicular, their slopes must be reverse opposites, which means that the slope of one of the equations will be the negative reciprocal of the slope of the other equation.
For example, if one of the equations has a slope m=2, the slope of a perpendicular line will be m= -1/2
The equations are:
Equation 1: 4y+24=0
Equation 2: 4x-28=0
Write the first equation for y:
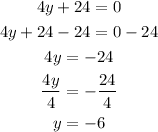
Write the second equation for x:
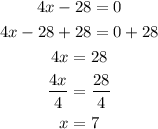
The first equation is a horizontal line at y=-6 and the second equation is for a vertical line at x=7. Since the first line is parallel to the x-axis (its slope is equal to zero) and the second line is parallel to the y-axis (it' slope is undetermined) you can conclude that both lines are perpendicular.