Question

PLEASE HELP ME I NEED HELPThe smith family is designing new plans for an in ground pool. Mr. Smith draws a rectangular shape with a length that is 5 feet longer than the height. A.) write a polynomial expression in simplified form, that represents the area of the pool. Show and explain how you got the area of the pool. Mrs. smith wants to add 2 foot concrete walkway around the edge of the pool. B.) Write a polynomial expression , in simplified form, that represents the total area of the pool and walkway. Show and explain how you got the area of the pool and the walkway. Mr. smith is unhappy with the 2 foot concrete walkway around the edge of the pool. He decides to put a different width around the pool. The total area of the pool and the walkway is given by the polynomial W^2+17W+66, where W represents the width of the pool. C.) Determine the width of the new walkway. Show all your work. Explain why you did each step.

Answer 1

A)

Let the height of the rectangle be "h".

We know the length is 5 feet longer than the height (h). So, the length is "h + 5".

The diagram is kind of..

The area of a reactangle is length x height, so

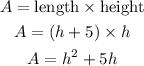
`\begin{gathered} A=\text{length}*\text{height} \\ A=(h+5_{})* h \\ A=h^2+5h \end{gathered}`B)

With the 2 feet wide concrete walkway all around the pool, we can draw...

The rectangle with pool & walkway has length >>> h + 5 + 2 + 2 = h + 9

The rectangle, with pool & walkway, has height >>> h + 2 + 2 = h + 4

Thus, the area is

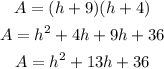
`\begin{gathered} A=(h+9)(h+4) \\ A=h^2+4h+9h+36 \\ A=h^2+13h+36 \end{gathered}`C)

Let the new width of the walkway be "x", and the height (width) of the pool is W, so the length and height of the POOL & WALKWAY is

Length = W+ 5 + x + x = W + 5 + 2x

Width = W + x + x = W + 2x

The area expression is >>>

`\begin{gathered} A=(W+5+2x)(W+2x) \\ A=W^2+2Wx+5W+10x+2Wx+4x^2 \\ A=W^2+4Wx+5W+10x+4x^2 \\ A=W^2+W(4x+5)+10x+4x^2 \end{gathered}`

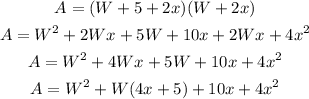
Now, matching it with the area expression given [W^2+17W+66], we can write an equation and solve for x,

`\begin{gathered} 4x+5=17 \\ 4x=17-5 \\ 4x=12 \\ x=(12)/(4) \\ x=3 \end{gathered}`

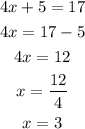
The new walkway is 3 feet in width (all around).