Question

The coordinate plane shows an arch that forms part of a bridge. Each unit represents 1 foot. Enter anequation of the quadratic function that models the arch, where x is the horizontal distance in feet fromthe left end and y is the height in feet for a given value of x. Complete the explanation of your answer.54(6,4)310,0)(12,0)431012The equation is y =Substitutefor h and 4 for k into the vertex form of a quadratic function: y = a (x -²+4.Then substitute 0 for x and 0 for y and solve for a: a =9

Answer 1

To find the equation of the function, we use

`y=a(x-h)^2+k`

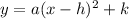
(h,k) is the vertex

Then, we we replace the values and find the value of "a"

`\begin{gathered} y=a(x-6)^2+4 \\ (12,0) \\ 0=a(0-6)^2+4 \\ a=-(4)/((-6)^2)=-(1)/(9) \end{gathered}`

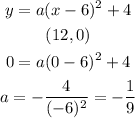
Finally, the equation is,

`y=(1)/(9)(x-6)^2+4`

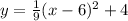
Subtitute 6 for h and 4 for k into the vertex form of a quadratic function: y = a(x-6)^2+4

Then substitute 0 for x and 0 for y and solve for a:a=-1/9