Question

An electron is accelerated by a potential difference of 3000V and enters a region of a uniform magnetic field. As a result the electron bends along a path with a radius of curvature of 26.0 cm.1. Find the speed of the electron in [Mm/s]as it enters the magnetic field.2. Find the magnitude of the magnetic field in [µT].3. Find the speed of the electron as it leaves the magnetic field in [Mm/s].

Answer 1

Given:

The potential difference, V=3000 V

The radius of the path of the electron, r=26.0 cm=0.26 m

To find:

1. speed of the electron as it enters the magnetic field.

2. Magnitude of the magnetic field.

3. Speed of the electron as it leaves the magnetic field.

Step-by-step explanation:

1.

The kinetic energy of the electron is,

`E_K=(1)/(2)mv^2=eV`

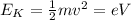
Where m is the mass of the electron, v is the velocity of the electron as it enters the magnetic field, and e is the charge of the electron.

On substituting the known values,

`\begin{gathered} (1)/(2)*9.1*10^(-31)* v^2=1.602*10^(-19)*3000 \\ \Rightarrow v=\sqrt[]{(2*1.602*10^(-19)*3000)/(9.1*10^(-31))} \\ v=32.5*10^6\text{ m/s} \\ =32.5\text{ Mm/s} \end{gathered}`

2.

The magnetic force provides the electron the neccessary centripetal force.

Thus,

`\begin{gathered} \text{evB}=(mv^2)/(r) \\ \Rightarrow B=(mv)/(er) \end{gathered}`

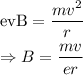
Where B is the magnetic field.

On substituting the known values,

`\begin{gathered} B=(9.31*10^(-31)*32.5*10^6)/(1.602*10^(-19)*0.26) \\ =7.26*10^(-4) \\ =726\text{ }\mu T \end{gathered}`

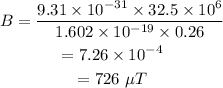
3.

The magnetic force acts on the electron in the direction perpendicular to its direction of motion. The magnetic force applied only changes the direction of the velocity and not its magnitude. Thus the velocity of the electron when it leaves the magnetic field is the same as its velocity when it enters the magnetic field.

Final answer:

1. The velocity of the electron when it enters the magnetic fields is 32.5 Mm/s

2. The magnitude of the magnetic field is 726 μT

3. The velocity of the electron when it leaves the magnetic field is 32.5 Mm/s