N=10 p=0.7 x=8 P(8)=A binomial probability experiment is conducted with the given parameters. Compute the probability of X successes in the end independent trials of the experim…

Question

asked Apr 25, 2023 190k views

1 Answer

John Chadwick · Answer 1 · 2023-04-28T23:08:01+0000

The formula to compute the binomial probability is given to be:

$P(x)={{{{n\choose x}}}}p^x(1-p)^(n-x)$

where

$\begin{gathered} n=\text{ number of trials} \\ p=\text{ probability} \\ x=\text{ number of successes} \end{gathered}$

The binomial coefficient is defined by:

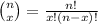
${{{{{n\choose x}}}}}=(n!)/(x!(n-x)!)$

The parameters provided in the question are:

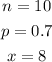
$\begin{gathered} n=10 \\ p=0.7 \\ x=8 \end{gathered}$

Therefore, we can begin solving by calculating the binomial coefficient:

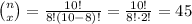
${{{n\choose x}}}=(10!)/(8!(10-8)!)=(10!)/(8!\cdot2!)=45$

Hence, we can calculate the probability to be:

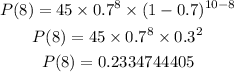
$\begin{gathered} P(8)=45*0.7^8*(1-0.7)^(10-8) \\ P(8)=45*0.7^8*0.3^2 \\ P(8)=0.2334744405 \end{gathered}$

ANSWER:

In 3 decimal places, the probability is 0.233.