We have to write a problem using rate, time and distance as the context that can be solved with the equation given.
We can start by relating rate (speed), time and distance:
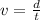
this equation represents the average speed, that can be calculated as the quotient between the distance and time.
We can also write, derived from the previous equation:
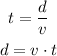
The equation t = d/v can be useful in this case, as we can let x represent distance, 1/2 represent total time and 6 and 4 represent speed in different parts of a path.
We then can write something like:
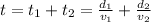
For example a trip between places A and C. There is a place between A and C, called B.
We walk from A to B at 6 km/h and then from B to C at 4 km/h. It takes half an hour (1/2 hour) to get from A to C.
We also know that the distance from B to C is one kilometer less than the distance from
A to B.
The question is: what is the distance from A to B?
Let x be the distance from A to B.
We can write this problem as:
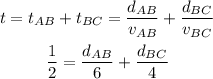
As the distance from B to C is one km less than from A to B we can write:
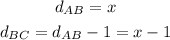
replacing in the equation, we get:
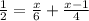
that is equivalent to the equation given.
Answer:
The problem can be stated as:
"We have to go from A to C. There is a place between A and C, called B.
We walk from A to B at 6 km/h and then from B to C at 4 km/h. It takes half an hour (1/2 hour) to get from A to C.
We also know that the distance from B to C is one kilometer less than the distance from A to B.
The question is: what is the distance from A to B?"