Question

1a) Bottled Drinking Water Americans drank an average of 23.2 gallons of bottled water per capita in 2004. If the standard deviation is 2.7 gallons and the variable is normally distributed, find the following probabilities. Use a graphing calculator and round the answers to four decimal places.More than 25 gallons of bottled water.p (more than 25 gallons of bottled water)=?

Answer 1

Given in the question:

a.) Mean = 23.2 Gallons

b.) Standard Deviation = 2.7 Gallons

p (more than 25 gallons of bottled water) = ?

We will be using the z - score formula:

`z\text{ = }\frac{(x\text{ -}\bar{\text{ x}})}{\sigma}`

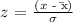
We get,

`z\text{ = }\frac{(x\text{ -}\bar{\text{ x}})}{\sigma}`
`z\text{ = }\frac{(25\text{ - }23.2)}{2.7}\text{ = }(1.8)/(2.7)`
`\text{ z = 0.67}`

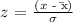
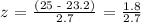
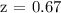
Applying the table,

At z = 0.67, the Probability = 0.2486.

Therefore, Probabilty = 0.2486.