Question

Supposed the salaries for recent graduates of one University have a mean of $24,800 with a standard deviation of $1100. Using Chebyshevs theorem what is the minimum percentage of recent graduates who have salaries between $21,500 and $28,100 Round your answer to one decimal place

Answer 1

The Solution:

Given:

`\begin{gathered} \mu=\text{ \$}24800 \\ \\ \sigma=\text{ \$}1100 \\ \\ Lower\text{ limit}=\text{ \$}21500 \\ \\ Upper\text{ limit}=\text{ \$}28100 \end{gathered}`

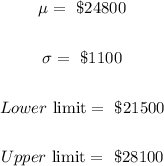
Required:

To find the minimum percentage of recent graduates who have salaries between $21,500 and $28,100.

Step 1:

We need to compute:

`Pr\left(21500≤X≤28100\right)`

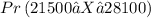
Notice that in this case:

`\begin{gathered} (Upper−μ)/(\sigma)=(28100-24800)/(1100)=3 \\ \\ (μ−Lower)/(\sigma)=(24800-21500)/(1100)=3 \end{gathered}`

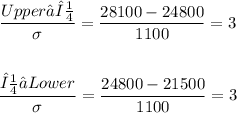
Since these two values coincide, it means that the event (21500, 28100) is centered around the mean = $24800 and, also, the event 21500≤X≤28100) is equivalent to having the sample mean to be within 3 standard deviations of the mean.

Apply the Chebychev theorem:

The probability that X is within k standard deviations of the mean can be estimated as follows:

[tex]Pr\left(∣X−μ∣In this case, since k=3, the probability that X is within 3 standard deviations from the mean is at least:[tex]\begin{gathered} Pr(X-\mu|Thus, the minimum percentage of the specified recent graduates is 88.9%