To determine the inequality, the first step is to determine the equation of the line.
The first step is to determine the slope. For this you have to use two points of the line, for example, points (2,-1) and (5,0) and the following formula:

Where
(x₁,y₁) are the coordinates of one point of the line.
(x₂,y₂) are the coordinates of a second point of the line.
Using (5,0) as (x₂,y₂) and (2,-1) as (x₁,y₁), you can calculate the slope as follows:
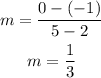
Once you have the value of the slope, using the point-slope formula you can determine the equation of the line:

(x₁,y₁) are the coordinates of one point.
m is the slope
Using m=1/3 and (x₁,y₁)=(5,0)
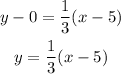
Distribute the multiplication on the parentheses term:
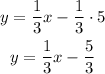
Pass the x-term to the left side of the expression by applying the opposite operation to both sides of it:
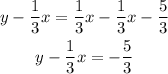
Multiply both sides of the expression by -3 to express the coefficient of the x-term as a positive integer:
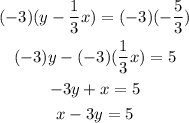
Next, note that the shaded area is above the line and that the line is dotted. The dotted line indicates that the values on the line are not included in the inequality.
The shaded area indicates that the values included in the inequality are those less than the values on the line, so the symbol to use for the inequality is " < ", and the inequality that corresponds to the graph is:
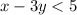
Second option.