SOLUTION
To get the best estimate, let's perform subtraction of the fractions
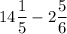
First, let us change the mixed fractions to improper fractions, we have
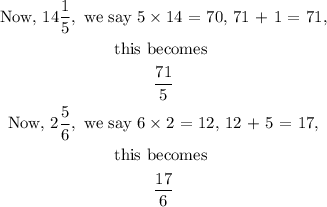
Subtracting the improper fractions we have

Breaking the fraction we have
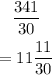
Looking at the options, the closest to this is 11, option B