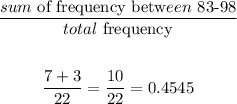Question

Need help solving this problem Note : 0.23 and 0.32 came back incorrect

Answer 1

A relative frequency is the ratio (fraction or proportion) of the number of times a value of the data occurs in the set of all outcomes to the total number of outcomes.

From the graph, the total frequency is

`\begin{gathered} 67-74=5 \\ 74-82=5 \\ 83-90=7 \\ 91-98=3 \\ 99-106=2 \\ sum\text{ of frequency =5+5+7+3+2=22} \end{gathered}`

Hence

The relative frequenc for 75-82 is

`\begin{gathered} \frac{Frequency\text{ of 75-82}}{total\text{ frequency}} \\ \\ (5)/(22)=0.2273 \end{gathered}`

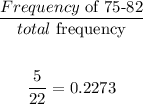
Therefore

The relative frequenc for 75-82 is 0.2273

The relative frequency for the interval of the score 83-98 is

`\begin{gathered} \frac{sum\text{ of frequency betw}een\text{ 83-98}}{total\text{ frequency}} \\ \\ (7+3)/(22)=(10)/(22)=0.4545 \end{gathered}`