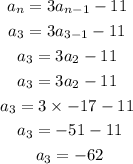Question

The following sequence is given in recursive form . what is the value of the third term

Answer 1

Given

The first term of the sequence is given by

`a_{1\text{ =}}-2`

`\begin{gathered} \text{For the other terms n, such that n }\ge\text{ 2} \\ a_n=3a_(n-1)-11\text{ } \end{gathered}`

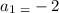
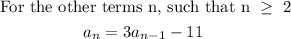
To get the third term, we will need to follow the following steps:

Step1: Obtain the second term

=> This will be obtaine

`\begin{gathered} a_2=3a_(2-1)-11\text{ } \\ a_2=3a_1-11\text{ } \\ a_2=3*-2_{}-11\text{ } \\ a_2=-6_{}-11\text{ } \\ a_2=\text{ -1}7 \end{gathered}`

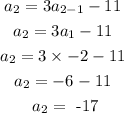
Step 2: Obtain the third term

=>This will be gotten by substituting the value of the second term into the equation

`\begin{gathered} a_n=3a_(n-1)-11\text{ } \\ a_3=3a_(3-1)-11\text{ } \\ a_3=3a_2-11\text{ } \\ a_3=3a_2-11\text{ } \\ a_3=3*-17_{}-11\text{ } \\ a_3=-51_{}-11 \\ a_3=-62 \end{gathered}`