We have to find the expression for the profit in function of the number of units x.
We have an expression for the revenue R(x) and for the cost C(x):
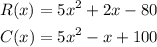
If the profit, that we will call P(x), is the difference between the revenue and the cost, we can calculate it like this:
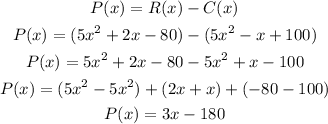
We can now calculate the profit for the sale of 1000 videogames (x = 1000) as:
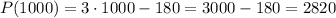
Answer:
a) P(x) = 3x - 180
b) The profit is $2820