Answer:
(Choice E) E Scalene triangle and (Choice F) F Obtuse triangle
Explanation:
Aside from E, Scalene triangle (as all the sides are of different lengths, we can assume that the angles will also be), the answer can either be B, Isosceles triangle or F, Obtuse triangle, so let's figure that out using the cosine rule! If it is an obtuse triangle, this means Angle ABC is bigger than Angle BAC and Angle BCA. But we can clearly see it is, as it's an Obtuse Triangle is a triangle where 1 angle is bigger than 90 degrees. Let's work out Angles BAC and BCA to find out if the triangle is obtuse or isosceles.
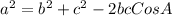This is the cosine rule formula. Now all we need to do is substitute in the values. We are using the cosine rule because we aren't given any angle values. We use Further Trigonometry instead of SOHCAHTOA as this clearly isn't a right-angled triangle. SOHCAHTOA only applies to triangles with a 90 degree angle, also known as a right-angled triangle. Let's rearrange the cosine formula so that we have everything equal to A instead.
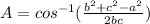
We will work out BAC first.
a = 5
b = 4
c = 7
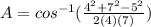
A = 44.4 rounded to 3 significant figures
Next, we will work out BCA.
a = 4
b = 5
c = 7
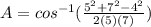
A = 34.0 rounded to 3 significant figures
The answer is F, Obtuse triangle and E, Scalene triangle
If we just worked out BAC, we would have noticed that by assuming BCA was also 44.4, the obtuse angle would be 91.2 degrees, which is barely above 90 degrees, therefore we would have correctly guessed the triangle as obtuse from there-on. I just worked out BCA as evidence to support that Triangle ABC cannot be isosceles, therefore we can eliminate that option and classify this triangle as Obtuse.
I hope my explanation helps!!