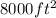Step-by-step explanation:
Part A:
To figure out the amount of fencing needed to enclose the plot, we will use the formula of the perimeter of a rectangl below
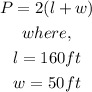
By substituting the values, we will have
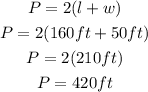
Hence,
The amount of fencing needed to enclose this plot will be
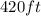
Part A:
The total area nclose by the fencing
This will be calculated using the formula for th area of a rectangle given below as
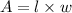
By substituting values, we will have
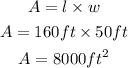
Hence,
The total area enclosed by this fencing is