Question

Graph this line using intercepts. A graph with the final answer would be greatly appreciated

Answer 1

Explanation:

Given the equation of the line:

`7x+9y=63`

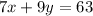
To graph the line, first, we determine the intercepts.

When x=0:

`\begin{gathered} 7x+9y=63 \\ 7(0)+9y=63 \\ \begin{equation*} 9y=63 \end{equation*} \\ (9y)/(9)=(63)/(9) \\ y=7 \end{gathered}`

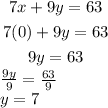
The y-intercept is at (0, 7).

When y=0:

`\begin{gathered} \begin{equation*} 7x+9y=63 \end{equation*} \\ 7x+9(0)=63 \\ 7x=63 \\ (7x)/(7)=(63)/(7) \\ x=9 \end{gathered}`

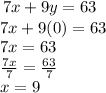
The x-intercept is at (9, 0).

Join the points (0, 7) and (9,0) to plot the line as shown below: