Exponential Decay
The rate of decay of radioactive material is proportional to its actual mass. When solving the resulting equation, we get the mathematical model as follows:
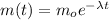
Where mo is the initial mass, λ is a constant, and t is the time.
The half-life time is the time it takes for the initial mass to be halved, i.e., the remaining mass is mo/2. Substituting into the formula for t=14 days:
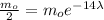
Simplifying by mo and solving for λ:
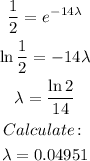
Now our model is complete:
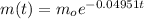
Now we are given the initial mass of a sample mo = 500 grams. It's required to calculate the remaining mass after t = 5 weeks = 5*7 = 35 days.
Substitute values:

Approximately 88 grams of the sample will remail after 5 weeks