Question

The annual salaries of employees in a large companyare approximately normally distributed with a mean of$50,000 and a standard deviation of $20,000.a.What percent of people earn less than $40,000?b.What percent of people earn between $40,000 and $70,000?c.What percent of people earn more than $70,000?

Answer 1

Let x be the normal variable denoting the annual salaries of employees

a) Probability of people earning less than $40,000 is given by:

`P(x<40000)=P(z<(40000-50000)/(20000))`

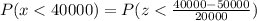
then:

`=P(z<(-10000)/(20000))=P(z<(-1)/(2))=P(z<-0.5)`

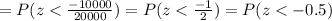
From z tables

`=0.3085`

Thus, in percent 0.3085 x 100 = 30.85%

Answer: People earn less than $40,000 is 30.85%

Graph

b) Probability of people earning between $40,000 and $70,000 is:

This is in percent 0.5328 x 100 = 53.28%

Answer: 53.28% of people earn between $40,0000 and $70,000

Graph

c) Probability of people earning more than $70,000 is:

`P(x>70000)=1-P(z<(70000-50000)/(20000))`

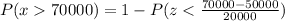
Then

`=1-P(z<(20000)/(20000))=1-P(z<1)`

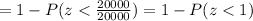
From z tables

`=1-0.8413=0.1587`

In percent is 0.1587 x 100 = 15.87%

Answer: The percent of people who earn more than $70,000 is 15.87%

Graph