We have to transform this word problem into an equation.
• Let's call ,x, to the money invested at 11% of annual interest.
,
• The money invested at 14% of annual interest is x+3000.
,
• The addition of these two invested amounts is equivalent to 1670 because that's the return.
The equation is
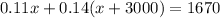
Solve for x.

Therefore, Mr. Ballew invested $5000 at 11% annual interest.
Add to obtain the other amount.
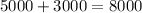
Therefore, Mr. Ballew invested $8000 at 14% annual interest.