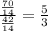To answer this question, we need to know that there were a total of 112 burgers that Saturday.
We have a part-to-part comparison of 5 burgers with everything to 3 with just cheese. That is:
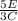
Where E is burgers with Everything and C is burgers with only cheese. However, we need to know the part-to-whole comparison, that is, how many are, respect to the total, burgers with everything, and how many are only cheeseburgers. For this, we need to do as follows:
Total = 5 + 3 = 8. Then, the burgers that are with cheese (from the total) is:

And the burgers with everything is:
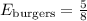
This is a ratio in a part-to-whole comparison.
Then, to the question: How many burgers topped with just cheese were made that day? We can answer as follows (BurgerFi made a total of 112 burgers that day):
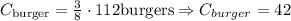
Therefore, there were 42 burgers topped with just cheese that day (Option 2.)
Checking the answer
We can check this if we get the total burgers with everything that were made that day:
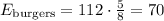
Then, if we compare those burgers into a part-to-part comparison, we must have the same ratio given in the question: 5 : 3. Then, we have:
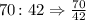
We have that the greatest common factor between 70 and 48 is 14. Then, if we divide the numerator and the denominator by 14, we have: