Question

The range of a battery off a newly electric vehicle is normally distributed with an average of 400 miles and a standard deviation of 20 miles. Find the probability a new vehicle off the assembly has a battery range greater than 420 miles? A) 0.84 B) 0.86 C) 0.16 D) 0.34

Answer 1

We can answer this question using the standard normal distribution. We need to "transform" the raw values into z-scores, and then consult a standard normal table to find the requested cumulative probability.

Finding the z-score

To find this value, we can proceed as follows:

`z=(x-\mu)/(\sigma)`

In this question, we have that:

`\mu=400,\sigma=20`

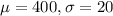
And we have that the raw value is equal to x = 420. Then, we have that the z-score, in this case, is:

`z=(420-400)/(20)=(20)/(20)=1`

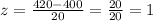
We have that the z-score is one standard deviation from the mean. Then, we have that this value represents a cumulative value of 0.84134. However, this is the cumulative probability for values less than 420.

Therefore, the actual value is:

`P(x>420)=1-0.84134=0.15866`

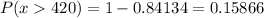
If we round this value to the nearest hundredth, we finally have that the probability is, approximately equal to 0.16 (option C).