ANSWER
PS = 47 units
Step-by-step explanation
We have the perimeter of this rectangle and we have to find the length of the side PS.
The perimeter of a rectangle is the sum of the lengths of the sides or the sum of twice each dimension - this is because the sides have the same length in pairs.
For this rectangle, we have that the perimeter is 198 units,
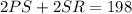
And sides PS and SR are (4y + 3) and (5y - 3) respectively. Replace into the equation above,
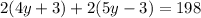
We have an equation for y. To solve it first we have to apply the distributive property,
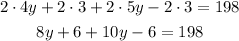
Then, add like terms,
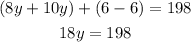
And finally, divide both sides by 18,
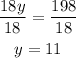
We now have y = 11, so we can replace it into the expression for the length of side PS,

The length of the side PS is 47 units.