Given,
The initial speed of the box, u=10 m/s
The coefficient of kinetic friction of the box, μ=0.4
The distance covered by the box, d=10 m
The acceleration acting on the box due to the kinetic friction between the box and the surface on which it is moving is given by,
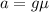
Where g is the acceleration due to gravity.
On substituting the known values,
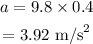
But this is the deceleration, i.e., the acceleration is in the opposite direction of the motion of the box as friction is the force that opposes the motion of an object.
Thus, a=-3.92 m/s²
From the equation of motion,

Where v is the final velocity, i.e., velocity after covering 10 m, of the box.
On substituting the known values,
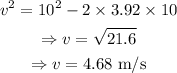
Thus the speed of the box after covering a distance of 10 m is 4.68 m/s