Question

Write an equation for a line parallel to y=2x−1 and passing through the point (2,1)

Answer 1

y = 2x-3

Explanation:

By definition, two lines are parallel if they have the same slope.

Given the equation for a line:

`y=2x-1`

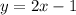
Comparing the given line with the slope-intercept form of a line:

`\begin{gathered} y=mx+b \\ \implies\text{Slope of the line, m=2} \end{gathered}`

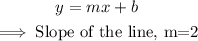
Thus, we want to find the equation of the line with the following properties:

• Slope: m = 2

,

• Point: (x1,y1)=(2,1)

In order to do this, we employ the use of the point-slope form of the equation of the line:

`\begin{gathered} y-y_1=m\mleft(x-x_1\mright) \\ \implies y-1=2(x-2) \end{gathered}`

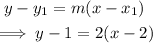
We then simplify:

`\begin{gathered} y-1=2x-4 \\ Add\text{ 1 to both sides of the equation} \\ y-1+1=2x-4+1 \\ y+0=2x-3 \\ y=2x-3 \end{gathered}`

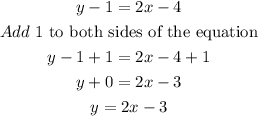
The equation of the parallel line is y=2x-3.