Question

A basketball team played 62 games. They won 30 more than they lost.A) How many games did they win? : ______B) How many games did they lose? : ______

Answer 1

We have from the question the following information:

• A basketball team played 62 games

,

• A basketball team won 30 more than they lost

And we need to find:

• The number of games the basketball team won

• The number of games the basketball team lost

To find these numbers, we have:

1. We can label the games the team won as x.

2. We can label the games the team lost as y.

3. The sum of the games the basketball team won and lost is:

`x+y=62\text{ \lparen First equation\rparen}`

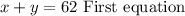
4. Since the team won 30 more games than they lost, we can say that:

`x=y+30`

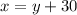
5. And now, we can find the number of games they lost by substituting the last equation in the first equation as follows:

`\begin{gathered} x+y=62\Rightarrow x=y+30 \\ \\ (y+30)+y=62 \\ \\ \text{ Adding like terms, we have:} \\ \\ y+y+30=62 \\ \\ 2y+30=62 \end{gathered}`

6. Now, we can subtract 30 from both sides of the equation, and then we have to divide the result by 2 as follows:

`\begin{gathered} 2y+30-30=62-30 \\ \\ 2y=32 \\ \\ (2y)/(2)=(32)/(2) \\ \\ y=16 \end{gathered}`

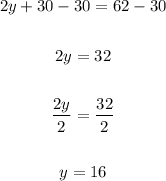
Therefore, the basketball team lost 16 games.

7. To find the number of games the team won, we can substitute this result in the first equation as follows:

`\begin{gathered} x+y=62 \\ \\ x+16=62 \\ \\ \text{ } \end{gathered}`

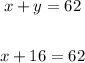
8. If we subtract 16 from both sides of the equation, we have:

`\begin{gathered} x+16-16=62-16 \\ \\ x=46 \end{gathered}`

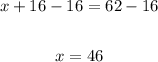
Then the basketball team won 46 games.

9. We can check the result using the first equation:

`\begin{gathered} x=46,y=16 \\ \\ x+y=62 \\ \\ 46+16=62 \\ \\ 62=62\text{ This is True.} \end{gathered}`

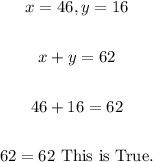
Therefore, in summary, we have that:

A) How many games did they win? : 46

B) How many games did they lose? : 16