Question

The position of a particle moving along the x axis is given by x = 6.0t 2 - 1.0t 3, where x is in meters and t in seconds. What is the position of the particle when it achieves its maximum speed in the positive x direction?

Answer 1

Answer:

The position of the particle when it achieves its maximum speed in the positive x direction is 20 meters

Step-by-step explanation:

The position of the particle is given by the equation

`x=6t^2-t^3`

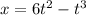
The speed (v) of the particle is calculated as:

`\begin{gathered} v=(dx)/(dt) \\ v=12t-3t^2 \end{gathered}`

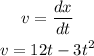
The acceleration of the particle is:

`\begin{gathered} a=(dv)/(dt) \\ a=12-6t \end{gathered}`

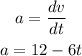
At maximum speed, the acceleration of the particle is zero

That is, a = 0

a = 12 - 6t

0 = 12 - 6t

6t = 12

t = 12/6

t = 2

This means that the speed of the particle is maximum at the time, t = 2

Substitute t = 2 into x = 6t² - t³

x = 6(2²) - (2²)

x = 6(4) - 4

x = 24 - 4

x = 20 meters

The position of the particle when it achieves its maximum speed in the positive x direction is 20 meters