In order to graph each parabola, first let's identify the vertex of each one.
To do so, let's compare them with the vertex form of the quadratic equation:

Where the vertex is located at (h, k).
For f(x), we have h = 0 and k = 0, so the vertex is at (0, 0).
For g(x), we have h = -4 and k = 0, so the vertex is at (-4, 0).
For h(x), we have h = 4 and k = 0, so the vertex is at (4, 0).
Now, to graph these functions, we need another point for each one.
Let's use x = 1 in each function and calculate the value of y:
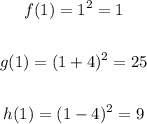
Graphing each parabola using the vertex and the additional point, we have:
(red = f(x), blue = g(x), green = h(x))
The effect of adding a positive constant h (if we have p(x) = (x + h)²) is moving the vertex left by h units.
The effect of adding a positive constant h (if we have p(x) = (x - h)²) is moving the vertex right by h units.