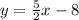Given:
The point A = (2,-3)
The equation given is 2x +5y =4
We will obtain the slope (m1) from the equation of the line since the line with point (2,-3) is perpendicular to the equation.
The rule for perpendicularism is,
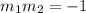
Isolate y from the equation

The equation of a line is written in the form

Therefore,
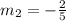
Let us now obtain m1
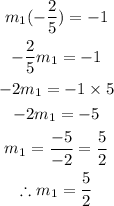
The formula for the equation of a line given a point is,

Where,
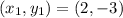
Therefore,
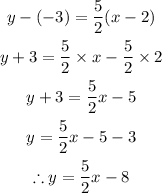
Hence, the equation of the line is,